Back to articles & videos

Unpacking Rosenshine's 10 Principles of Effective Instruction

Maths Trek 20/2/25

Educators seeking to enhance their teaching impact often turn to evidence-based frameworks for guidance in refining their instructional methods.

Barak Rosenshine’s Principles of Instruction has become a cornerstone of effective teaching, celebrated for its evidence-based, adaptable framework grounded in cognitive science, research and classroom observation.

These principles emphasise clarity, active engagement and consistent reinforcement. This aligns with what educators intuitively know about effective teaching while offering a structured approach to refine their methods. When implemented thoughtfully, these principles can provide guidance for fostering deep, lasting learning in your classroom.

So with this in mind, let’s take a closer look at what these principles are and how Maths Trek helps you implement them.

Overview

There are 10 principles:

1. Daily review
2. Present new material using small steps
3. Ask questions
4. Provide models and worked examples
5. Guide student practice
6. Check for student understanding
7. Obtain a high success rate
8. Provide scaffolds for difficult tasks
9. Independent practice
10. Engage in regular reviews

It’s important to remember that you don’t have to achieve all 10 principles in a single lesson! Instead, it’s about comprehensively integrating these principles across the year.

Daily reviews

Daily reviews are currently a hot topic among Australian educators. According to Rosenshine, the idea of daily review is to conduct a short review of previously learned content to help strengthen previous knowledge and build fluency.

Daily reviews are particularly important for teaching material that will be used in subsequent learning such as maths facts and math computation – concepts that need to become automatic. They should be completed quickly, leaving plenty of time for the lesson ahead.

Maths Trek includes tools and resources you can draw from to conduct quick and engaging daily reviews with your students. These include Daily Number Practice activities to support fluency when using the four operations, as well as access to interactive tools such as place value charts and hundreds charts to review previously learnt skills in interesting ways.

Present new material using small steps

Our working memory, the place where we process information, is small and can only handle a few bits of information at a time. Too much information swamps our working memory.

In his findings, Rosenshine explains, ‘The more successful teachers did not overwhelm their students by presenting too much new material at once.’ Rather, these teachers only present small amounts of new material, then assist students as they practise this material.

Maths Trek’s sequence of topics, problem-solving lessons and investigations have been purposefully spaced to ensure material is delivered at a manageable pace and is built upon throughout the year. This scaffolding boosts student’s capacity and confidence in tackling new challenges.

What’s more, within a given lesson, Maths Trek teaching slides are carefully paced to present information incrementally and to scaffold the student learning experience.

Ask questions

Rosenshine emphasises the importance of questioning as a tool for active learning. Thoughtful questions engage students, test understanding and identify misconceptions. By asking both open-ended and targeted questions, educators encourage deeper thinking and ensure all students are involved in the learning process.

While there are countless opportunities for questioning and discussions in Maths Trek, open-ended and targeted questions are provided in context. Every problem-solving practice unit includes targeted ‘what if’ questions to extend critical thinking about the original problem. Investigations include Focus/Guiding questions to help teachers check for understanding at each step. Topic lessons also feature open-ended and targeted questions where appropriate.

Provide models and worked examples

While Rosenshine’s principles can work for any subject, this particular principle is imperative when teaching maths and should be embedded in every maths lesson where possible.

Modelling is a powerful way to clarify abstract concepts or processes. Worked examples allow students to focus on the specific steps to solve problems. Effective models and worked examples help reduce the cognitive load for students when learning new information.

Maths Trek includes an abundance of worked examples that have been carefully crafted to ensure they’re clearly stepped out. They are presented in a format that allows students to focus on the information and are easy for teachers to use as a discussion prompt.

Check out this worked example slide sequence from Year 4, Unit 19.1 Addition:

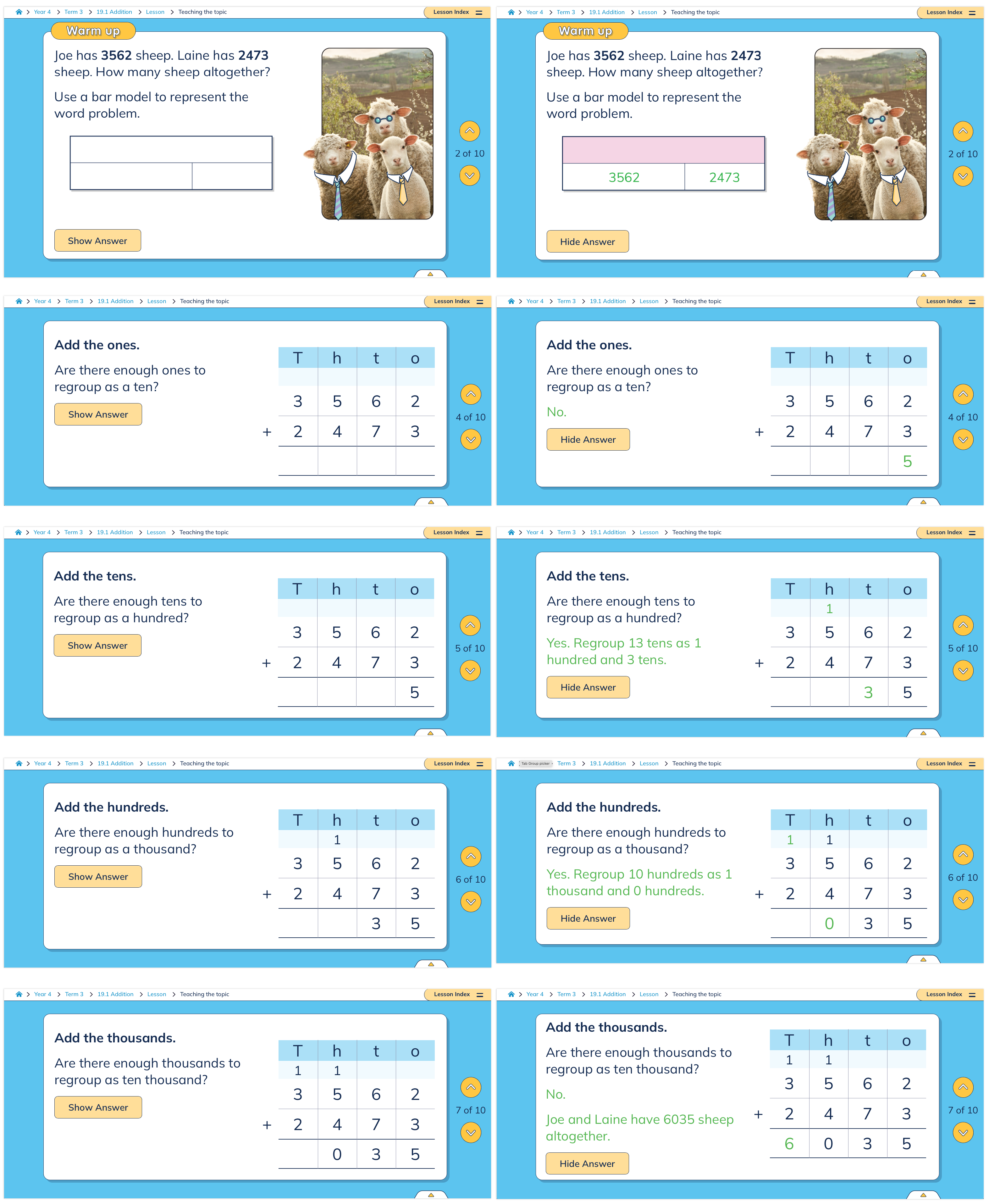
Guide student practice

While independent practice is important, guided practice ensures students are applying new knowledge correctly. Teachers should provide structured and collaborative opportunities for students to practise with immediate feedback. This reduces the risk of reinforcing errors and builds confidence in applying new skills.

Maths Trek follows the Gradual Release of Responsibility Framework, with structured ‘I Do, We Do and You Do’ components built into each lesson. During the ‘We Do’ or guided Work together part of the lesson, students work with the teacher to tackle questions based on what they’ve just been explicitly taught. The online teaching resource enables teachers to show correct answers with the click of a button. This allows for whole-class marking and time to address any misconceptions before moving on to independent practice of the same concept.

Check for student understanding

Effective teaching involves regularly assessing whether students have grasped the material. This can be done through informal checks like thumbs up/thumbs down, mini quizzes or class discussions. Frequent checks allow teachers to adjust their instruction in real time, ensuring no student is left behind.

There are many tools in Maths Trek that help you monitor student understanding along the way. For example, the Work together step in all topics allows teachers to check for on-the-spot understanding, whereas features like the Problem-Solving Progress Checklists guide teachers to track and jot down notes on student progress throughout the year. Investigations also include critical thinking questions, allowing students to reflect informally and provide teachers with opportunities for formative assessment.

Obtain a high success rate

Rosenshine suggests aiming for an 80% success rate during lessons. This ensures students are challenged but not overwhelmed. This doesn’t mean that all students are expected to achieve success at the same level of difficulty. Teachers should differentiate their instruction to obtain high success rates.

Maths Trek makes this easy by including differentiation tasks in each topic lesson for both support and extension students. The majority of topics in Years 3–6 also include a built-in challenge activity, which provides added extension for fast finishers.

Provide scaffolds for difficult tasks

Scaffolding is a critical strategy for tackling complex concepts or skills. It involves providing temporary supports, such as prompts, graphic organisers or sentence starters, to help students complete tasks. As students gain confidence, these scaffolds can gradually be removed, fostering independence.

Maths Trek includes scaffolds within lessons, including bar models to aid in addition and subtraction word problems, number expanders to support place value understanding and think boards to represent numbers in different ways. The program also provides many of these as printable resources. Instead of creating resources from scratch, teachers can download these scaffolds straight from their Maths Trek Online teacher access for immediate use with their class.

Independent practice

Rosenshine puts this simply, ‘The best way to become an expert is through practice – thousands of hours of practice. The more practice, the better the performance.’

But it’s not just about giving students plenty of practice – what leads into the practice and having access to the teacher during practice is also important. Research found that students were more engaged when their teacher circulated the room and monitored their work as long as the teacher didn’t spend extended periods of time with just one or two students. For this reason, independent practice should involve the same material as the guided practice (one of Rosenshine’s other principles), so that students are fully prepared for the activities, allowing teachers to effectively circulate the room during the practice period.

Maths Trek incorporates independent practice activities extensively throughout the program. And – critically – its lesson content and guided practice flow seamlessly into the independent practice activities.

Engage in regular reviews

Learning is a process of continual reinforcement. Rosenshine’s research identifies that ‘material that is not adequately practised and reviewed is easily forgotten’.¹

Regular reviews, whether weekly or monthly, help consolidate knowledge in students’ long-term memory. Cumulative reviews that revisit previously learnt concepts aid memory retention and allow students to see how concepts interconnect.

Maths Trek includes revision units that are regularly spaced throughout the year to assist with concept retrieval and to support successive relearning. In addition, a typical Maths Trek week includes four explicit lessons, leaving a day for consolidation/remediation and review as required.

If you’re interested to explore the Maths Trek program, head to our website, sign up for a free trial or contact your local education consultant.

References
1. Rosenshine, B 2012, ‘Principles of Instruction: Research-based strategies that all teachers should know’, American Educator, Spring 2012 pp. 12–39, https://www.aft.org/sites/default/files/Rosenshine.pdf↩

More Maths Trek articles & videos